Shadertoy Tutorial Part 3 - Squares and Rotation
Greetings, friends! In the previous article, we learned how to draw circles and animate them. In this tutorial, we will learn how to draw squares and rotate them using a rotation matrix.
How to Draw Squares
Drawing a square is very similar to drawing a circle except we will use a different equation. In fact, you can draw practically any 2D shape you want if you have an equation for it!
The equation of a square is defined by the following:
max(abs(x),abs(y)) = r
x = x-coordinate on graph
y = y-coordinate on graph
r = radius of square
We can re-arrange the variables to make the equation equal to zero:
max(abs(x), abs(y)) - r = 0
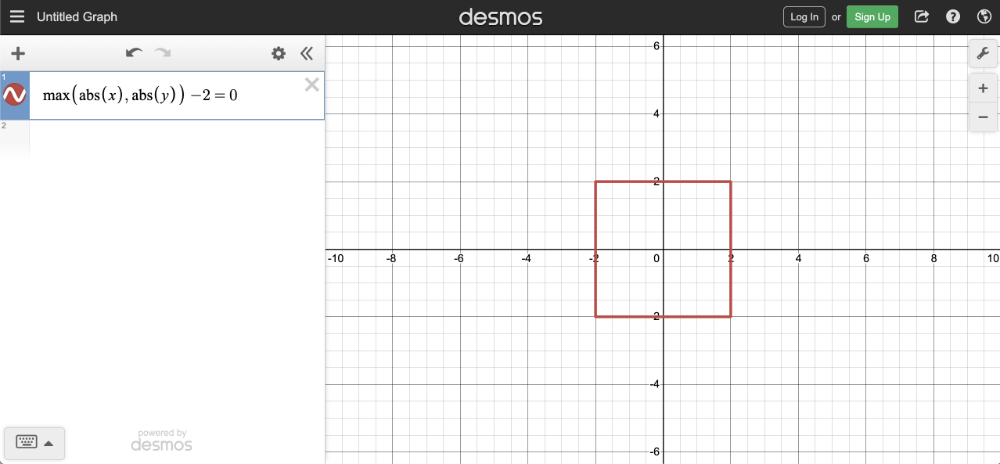
To visualize this on a graph, you can use the Desmos calculator to graph the following:
max(abs(x), abs(y)) - 2 = 0
If you copy the above snippet and paste it into the Desmos calculator, then you should see a graph of a square with a radius of two. The center of the square is located at the origin, (0, 0).
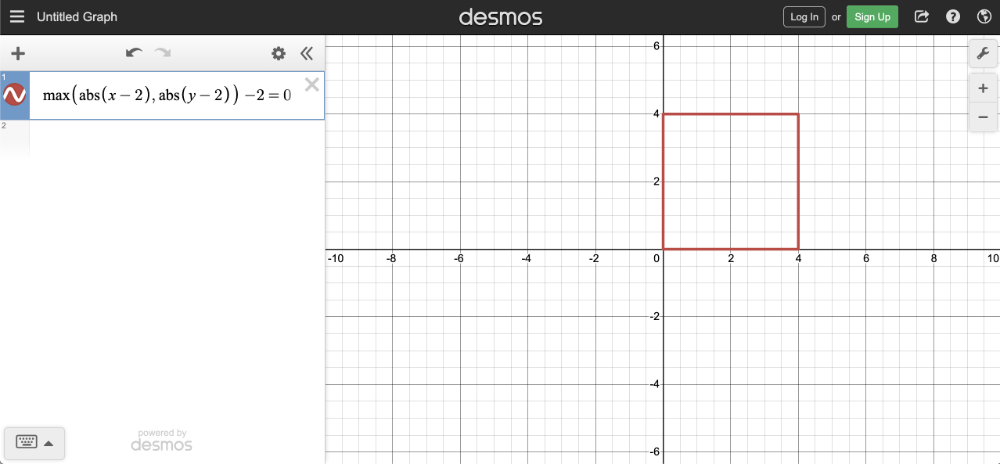
You can also include an offset:
max(abs(x - offsetX), abs(y - offsetY)) - r = 0
offsetX = how much to move the center of the square in the x-axis
offsetY = how much to move the center of the square in the y-axis
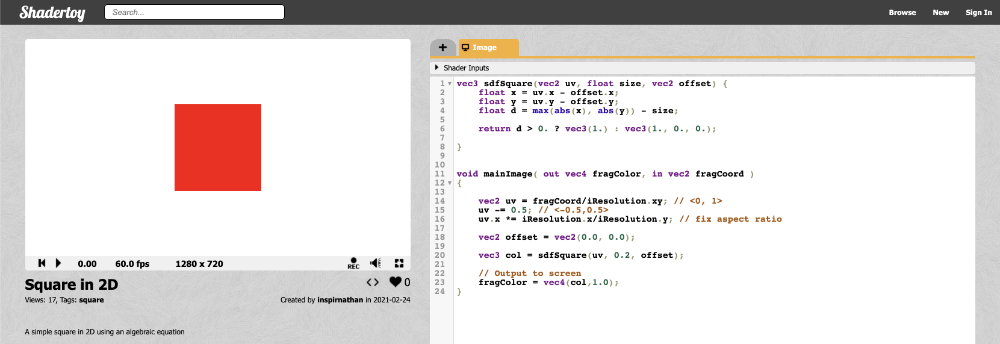
The steps for drawing a square using a pixel shader is very similar to the previous tutorial where we created a circle. Instead, we'll be creating a function specifically for a square.
vec3 sdfSquare(vec2 uv, float size, vec2 offset) {
float x = uv.x - offset.x;
float y = uv.y - offset.y;
float d = max(abs(x), abs(y)) - size;
return d > 0. ? vec3(1.) : vec3(1., 0., 0.);
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = fragCoord/iResolution.xy; // <0, 1>
uv -= 0.5; // <-0.5,0.5>
uv.x *= iResolution.x/iResolution.y; // fix aspect ratio
vec2 offset = vec2(0.0, 0.0);
vec3 col = sdfSquare(uv, 0.2, offset);
// Output to screen
fragColor = vec4(col,1.0);
}
Yay! Now we have a red square! 🟥
Rotating shapes
You can rotate shapes by using a rotation matrix given by the following notation:
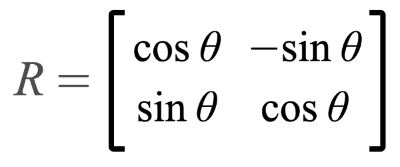
Matrices can help us work with multiple linear equations and linear transformations. In fact, a rotational matrix is a type of transformation matrix. We can use matrices to perform other transformations such as shearing, translation, or reflection.
We can use a graph I created on Desmos to help visualize rotations. I have created a set of parametric equations that use the rotation matrix in its linear equation form.
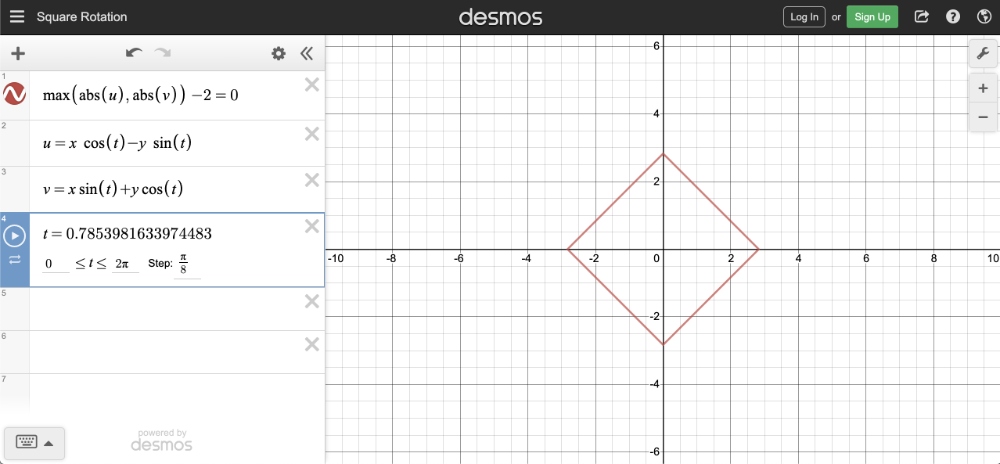
The linear equation form is obtained by multiplying the rotation matrix by the vector [x,y] as calculated by WolframAlpha. The result is an equation for the transformed x-coordinate and transformed y-coordinate after the rotation.
In Shadertoy, we only care about the rotation matrix, not the linear equation form. I only discuss the linear equation form for the purpose of showing rotations in Desmos.
We can create a rotate function in our shader code that accepts UV coordinates and an angle by which to rotate the square. It will return the rotation matrix multiplied by the UV coordinates. Then, we'll call the rotate function inside the sdfSquare function by passing in our XY coordinates, shifted by an offset (if it exists). We will use iTime as the angle, so that the square animates.
vec2 rotate(vec2 uv, float th) {
return mat2(cos(th), sin(th), -sin(th), cos(th)) * uv;
}
vec3 sdfSquare(vec2 uv, float size, vec2 offset) {
float x = uv.x - offset.x;
float y = uv.y - offset.y;
vec2 rotated = rotate(vec2(x,y), iTime);
float d = max(abs(rotated.x), abs(rotated.y)) - size;
return d > 0. ? vec3(1.) : vec3(1., 0., 0.);
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = fragCoord/iResolution.xy; // <0, 1>
uv -= 0.5; // <-0.5,0.5>
uv.x *= iResolution.x/iResolution.y; // fix aspect ratio
vec2 offset = vec2(0.0, 0.0);
vec3 col = sdfSquare(uv, 0.2, offset);
// Output to screen
fragColor = vec4(col,1.0);
}
Notice how we defined the matrix in Shadertoy. Let's inspect the rotate function more closely.
vec2 rotate(vec2 uv, float th) {
return mat2(cos(th), sin(th), -sin(th), cos(th)) * uv;
}
According to this wiki on GLSL, we define a matrix by comma-separated values, but we go through the matrix column-first. Since this is a matrix of type mat2, it is a 2x2 matrix. The first two values represent the first column, and the last two values represent the second-column. In tools such as WolframAlpha, you insert values row-first instead and use square brackets to separate each row. Keep this in mind as you're experimenting with matrices.
Our rotate function returns a value that is of type vec2 because a 2x2 matrix (mat2) multiplied by a vec2 vector returns another vec2 vector.
When we run the code, we should see the square rotate in the clockwise direction.

Conclusion
In this lesson, we learned how to draw a square and rotate it using a transformation matrix. Using the knowledge you have gained from this tutorial and the previous one, you can draw any 2D shape you want using an equation or SDF for that shape!
In the next article, I'll discuss how to draw multiple shapes on the canvas while being able to change the background color as well.