Parser Generators for Math Expressions
Greetings, friends! This is my ninth post in the math expression parser series. Up until now, we've been relying on building a parser from scratch using our own implementation of the shunting yard algorithm. Well, that changes today! We will now start learning about parser generators to generate parsers automatically for us. But how does that work? Let's find out together!
Introduction to Parser Generators
Parser generators are tools that let people create parsers automatically without having to write much code. The basic idea is that they accept a special kind of input known as a grammar and outputs/generates a parser in a target programming language. In this tutorial series, we'll use a parser generator to create a math expression parser. We'll then use that parser to solve math expressions or build abstract syntax trees (AST).
A grammar refers to a file or group of text that contains a syntax for a language's rules. A grammar file may also contain information about how text is tokenized. Depending on the tool, the grammar file may contain rules on how to both tokenize and parse text. Super convenient!
The library author of a particular parser generator will normally document how to build grammars using their own syntax. We'll look into how to build grammars later.
On Wikipedia, you'll see lots weird math notation and theory behind grammars. I'll discuss what grammars are in simple terms in this tutorial, so don't worry about all the complex jargon.
Some parser generators create parsers in the target programming language you specify. In this tutorial series, we'll target the JavaScript language. Once we have a parser, we can use it to parse things as defined in our grammar. Our grammar will include all the rules necessary for tokenizing and building a math expression parser.
Here's a fun fact! Parser generators can be used to create an entire programming language. Even Python was originally created using an LL(1) parser generator called pgen! Starting in Python 3.9, a PEG-based parser generator called pegen was used to create a new Python parser.
As seen on Wikipedia, there are many different implementations of parser generators. Each one uses one or more different types of parsing algorithms. They can also output parsers in one or more programming languages. Even though a parser generator is coded in JavaScript, it can be designed such that it outputs a different programming language such as Ruby or Rust.
Grammars
As mentioned earlier, parser generators normally accept a particular kind of grammar. The author of a parser generator tool will typically tell you how to write grammars and what syntax to use.
There are many ways to express a grammar. The most common notations used for grammars are the following:
An author of a parser generator may use one of these three notations, or use their own custom notation for describing grammars. They may even let you write grammars using syntax similar to JSON or even programmatically using a programming language such as JavaScript.
Below is a simple grammar, expressed in Backus-Naur form (BNF), for handling addition and multiplication in math expressions.
expression : expression + expression
| expression * expression
| number
The : is like saying "can be derived into" and the | symbol is like saying "or". This grammar is saying an expression can be derived into a sum of expressions, a product of expressions, or a number.
Parsing Algorithms
When people implement parser generators, they usually use one or more types of parser algorithms. Parsing algorithms can generally be divided into two groups:
Top-down and bottom-up parsers can be implemented using a variety of algorithms. I'll only list a few for each type of parser.
Top-down Parsers
- LL(1)
- Recursive descent
- Pratt parsing (or Top-down Operator Precedence)
- Earley
- Packrat (used by PEG Parsers)
- Combinatory parsing (Parser Combinators)
Bottom-up Parsers
Choosing a Parsing Algorithm
At this point, you might be wondering why there are so many different algorithms used to create parsers. Isn't there one algorithm that is better than them all?
As with most algorithms in software development, the answer is "it depends." Each algorithm has their own sets of advantages and disadvantages. Some algorithms are faster than others, but they might consume more memory or accept a fewer amount of grammars.
Other algorithms such as GLR parsing have seen use in incremental parsers. Incremental parsers are optimized for parsing only a portion of text that the user changes to help speed up parsing. If you want syntax highlighting for your favorite programming language, then you may have encountered Tree-sitter and CodeMirror. These tools use incremental parsing and GLR parsing to help speed up parsing and handle many more types of grammars than CLR(1) or LALR(1) parsers.
In this tutorial series, we'll build a math expression parser five times using each of following types of parsers:
- LALR(1) parser (via parser generator)
- LL(1) parser (via parser generator)
- PEG parser (via parser generator)
- Recursive descent (manually)
- Pratt parsing (manually)
By rebuilding a math expression parser in different ways, we'll understand the pros and cons of each approach. Hopefully, the knowledge you gain in this tutorial series can also be applied toward building a custom programming language 😃
The LL(1) and LALR(1) parsers will be created using a parser generator. A parser generator will construct a parsing table that contains information about all the possible states the parser can be in. Then, it will use the parsing table to figure out how to resolve symbols and apply semantic analysis. That is, the parser will understand how to provide meaning to the tokens depending on where they occur in a given text.
In this tutorial series, we'll use a tool called Syntax for generating LL(1) and LALR(1) parsers. This tool was created by the talented Dmitry Soshnikov who happens to have amazing courses on parser theory.
For building a PEG parser, we'll use a JavaScript library called Peggy, formerly called PEG.js. Peggy is a parser generator that accepts a particular type of grammar called parsing expression grammar (PEG). PEG parsers can handle ambiguities automatically unlike LL and LR parsers.
The recursive descent and pratt parsers will be created manually without a parser generator. These algorithms will use recursion to parse through text, but it's important to understand how LL(1) parsers and grammars work first. We'll use our knowledge of grammars to help create a math expression parser using the recursive descent and pratt parsing algorithms.
LL and LR Parsers
LL(1) parsers are very common types of LL parsers. LALR(1) parsers are very common types of LR parsers.
The (1) means we use a single "lookahead" in the parsing algorithm. When we created a tokenizer in Part 5, our tokenizer had a method called getNextToken for retrieving the next token. We could technically "look ahead" at the next token.
If we had an LL(2) parser, then we could look ahead two tokens instead of one. The tradeoff is that it takes more time and memory to look at more tokens. Parsers that use more than one lookahead token are rare, so we're fine with using LL(1) and LALR(1) parsers that use a single lookahead token for most grammars.
The "LL" term refers to "left-to-right, leftmost derivation." This means the parser will scan a given input from the left to the right (beginning of text to the end of text). The parser will also attempt to create a leftmost derivation.
The "LR" term refers to "left-to-right, rightmost derivation." The parser will still scan a given input from left to the right, but LR parsers will attempt to construct a rightmost derivation.
What does leftmost and rightmost derivation mean? Let's look at an example.
Suppose we had the following math expression: 1 + 2 * 3.
When a parser reads through this math expression, it needs to understand how to derive this math expression using rules. A typical grammar for a math expression parser might look something like this:
expression : expression + expression
| expression * expression
| number
In the grammar above, we're using a notation called Backus-Naur Form (BNF).
Do you see what's happening? An expression can be one of three things according to our grammar:
- A sum of expressions
- A product of expressions
- A number
Using the above grammar and parsing tables generated by the parser generator, an LL parser will attempt to "derive" the math expression, 1 + 2 * 3, using leftmost derivation.
1. expression → expression + expression
2. → number + expression
3. → number + expression * expression
4. → number + number * expression
5. → number + number * number
6. → 1 + 2 * 3
Our entire math expression, 1 + 2 * 3 is an expression, but an expression actually consists of multiple expressions. 1 + 2 and 2 * 3 can also be considered expressions. An LL parser will use leftmost derivation, so it derives from left-to-right. In step 2, the first expression is derived as a number. Eventually, the second expression on the right of the + sign is derived as well.
Let's look at how a LR parser will attempt to derive the same math expression, 1 + 2 * 3, using rightmost derivation.
1. expression → expression + expression
2. → expression + expression * expression
3. → expression + expression * number
4. → expression + number * number
5. → number + number * number
6. → 1 + 2 * 3
Notice the difference? A LR parser is working backwards (or bottom-up). While it may not seem obvious right now, the act of performing leftmost derivation versus rightmost derivation can drastically change whether a parser will be able to accept a particular grammar without any conflicts.
In fact, LR parsers can actually accept substantially more types of grammars than LL parsers. Below is a Venn diagram of common LR parsers and a LL(1) parser. The larger the circle, the more grammars that are accepted by that particular kind of parser.
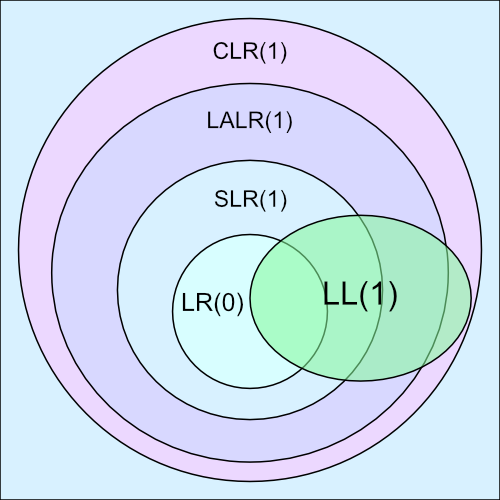
Notice that the CLR(1) parser accepts more than LALR(1) parsers. However, we'll typically see that LALR(1) parsers are good enough for handling most types of grammars. LL(1) parsers are simpler to construct, but they accept a lot less grammars than the other parser implementations. This is due to a common conflict called left recursion.
It's entirely possible to modify grammars to eliminate left recursion so that LL(1) parsers can accept them. However, by modifying a grammar, we are technically changing it to a different grammar.
Conflicts
When using a parser generator, we'll likely run into "conflicts." Common conflicts in LL Parsers include "first/first" conflicts and "first/follow" conflicts. Common conflicts in LR Parsers include "shift-reduce" conflicts and "reduce-reduce" conflict. We'll discuss conflicts later when we use the Syntax parser generator to build parsers out of our grammar files.
It's good to be aware that grammars may cause ambiguities. Both LL(1) and LALR(1) parsers, by default, don't know how to handle ambiguities. We'll discuss ambiguities in the next tutorial.
Usually, the author of a parser generator tool provides a few ways we can add extra data to a grammar so that the parser knows how to resolve conflicts automatically.
Common Parser Generator Tools
As mentioned earlier, this tutorial series will focus on using the Syntax parser generator for creating LL and LR parsers. However, there are other parser generator tools that exist for the JavaScript community. Some of the most common ones include:
Each of these parser generators implements different parsing algorithms. Therefore, they may or may not support LL or LR parsers.
The Jison parser generator is inspired by the GNU Bison parser generator. Jison is actually used by a variety of tools you might already be familiar with including Mermaid and the Handlebars.js parser.
Peggy is a parser generator used to build parsers that accept parsing expression grammars (PEG). It is used by a variety of tools including Kibana.
The predecessor to Peggy, PEG.js, has been used in a variety of tools as well including Markdoc.
For educational purposes, the Syntax parser generator is the most useful for learning how LL and LR parsers work. We can even use the LR parsing modes to build a fully functional math expression parser. The Syntax tool supports the following algorithms:
- LL(1)
- LR(0)
- SLR(1)
- LALR(1)
- CLR(1)
Conclusion
The world of parser theory is vast! It's certainly a big topic! Did I confuse you? Still with me? I hope I didn't scare anyone away 😅
Once we start using the Syntax tool in the next tutorial, things should hopefully make more sense. We'll build our first grammar and LR parser! We'll see how easy it is to make a parser compared to all the work we did with the shunting yard algorithm!
Until next time, happy coding! 🙂