Abstract Syntax Trees with the Shunting Yard Algorithm

#javascript#parsers
Published: Tuesday, February 28, 2023
Updated: Wednesday, March 1, 2023

Greetings, friends! This is my eighth post in the math expression parser series. In the previous tutorials, we've been building a math expression parser that evaluates math expressions and calculates a final result. In this tutorial, we'll learn how to build an abstract syntax tree (AST) instead of returning a calculated value. Let's begin!

Visualizing Abstract Syntax Trees

We briefly discussed abstract syntax trees (AST) in the first part of this math expression parser series. A tree is a type of data structure used to store, organize, and/or visualize data. An abstract syntax tree is just a type of tree that is used to represent "abstract" information such as binary operations in math expressions.

In the previous tutorials, we've been evaluating math expressions. For example, the math expression, 1 + 2 * 3, evaluates to the result, 7. Now, we would like to construct an AST instead. There are multiple ways we can represent tree data structures: JSON, XML, JavaScript objects, class-based objects, and more. In fact, even a file system can be thought of as a tree!

In this tutorial, we will create a tree data structure using a JavaScript object. For example, the AST for 1 + 2 will look like the following:

js
Copied! ⭐️ 
const ast = {
  type: 'BinaryExpression',
  operator: '+'
  left: {
    type: 'Number',
    value: 1
  },
  right: {
    type: 'Number',
    value: 2
  }
}

As you can tell, each node on the tree contains a type. If the node is a BinaryExpression, then it will contain four fields: type, operator, left, and right. If the node has a type of Number, then it will contain the fields: type and value.

The fields I have chosen to include in the AST are arbitrary yet useful. We can add whatever information we want to the tree. Remember, an AST is abstract! I have chosen the minimum amount of fields necessary for understanding how to recreate a math expression from an AST.

tip
Abstract syntax trees can be used to analyze the source code of various programming languages, not just math expressions! Check out AST Explorer to look at various ways we can build JavaScript ASTs!

Let's look at another example. Below is an AST for the math expression, 1 + 2 * 3.

js
Copied! ⭐️ 
const ast = {
  type: 'BinaryExpression',
  operator: '+'
  left: {
    type: 'Number',
    value: 1
  },
  right: {
    type: 'BinaryExpression',
    operator: '*',
    left: {
      type: 'Number',
      value: 2
    },
    right: {
      type: 'Number',
      value: 3
    }
  }
}

This math expression can be visualized as the following abstract syntax tree.

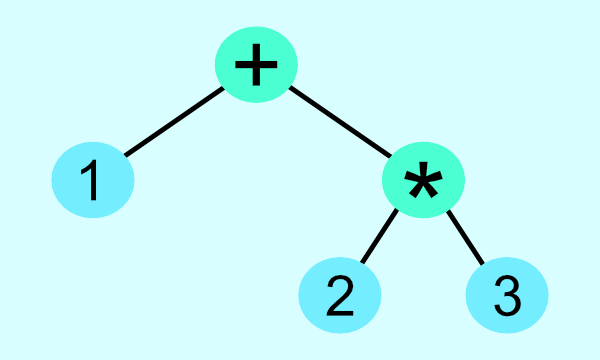
Abstract tree for one plus two times three.

The top node has the lowest priority, and the bottom nodes of the tree have the highest priority. As we can see from the AST above, multiplication is applied first followed by addition.

js
Copied! ⭐️ 
1 + 2 * 3 = 1 + 6 = 7

The math expression, 1 + 2 * 3, is a binary expression of a binary expression. The tree contains a number on the left side and a binary expression on the right side. The nested binary expression then contains a number node on both the left and right side. The AST will grow larger the longer the math expression is.

Building an AST with the Shunting Yard Algorithm

In the previous tutorial, we completed a math expression evaluator that can understand the following:

  1. Parentheses
  2. Addition
  3. Subtraction
  4. Multiplication
  5. Division
  6. Exponentiation
  7. Unary operations (for negative numbers)
  8. The sin function
  9. The cos function
  10. The tan function

Inside the math expression evaluator, we had a function called evaluate that was responsible for calculating a value when the user provides a math expression. Now, we would like to change the name of this function to generateAST and create an abstract syntax tree where each node represents one of the operations mentioned in the list above.

Luckily, most of our changes will occur in the handlePop function because that is where the main computations happen. Currently, this function looks like the following:

js
Copied! ⭐️ 
function handlePop() {
  const op = stack.pop()

  if (op === '(')
    return

  if (op === 'u')
    return -Number.parseFloat(output.pop())

  if (isFunction(op)) {
    const poppedValue = output.pop()
    switch (op) {
      case 'sin':
        return Math.sin(poppedValue)
      case 'cos':
        return Math.cos(poppedValue)
      case 'tan':
        return Math.tan(poppedValue)
    }
  }

  const right = Number.parseFloat(output.pop())
  const left = Number.parseFloat(output.pop())

  switch (op) {
    case '+':
      return left + right
    case '-':
      return left - right
    case '*':
      return left * right
    case '/':
      return left / right
    case '^':
      return left ** right
    default:
      throw new Error(`Invalid operation: ${op}`)
  }
}

Notice how we perform a particular mathematical operation and then return a result. Instead of returning a result, we will instead return an object that represents a node on our AST.

During binary operations such as addition or multiplication, we will return the following node. Since binary operations require two values, we'll create an AST node that contains a left and right field.

js
Copied! ⭐️ 
{
  type: 'BinaryExpression',
  operator: operator
  left: left
  right: right
}

During unary operations, we will return the following node. A unary operation only operates on a single value, so we can create an AST node that contains a value field.

js
Copied! ⭐️ 
{
  type: 'UnaryExpression',
  value: value
}

During function operations such as sin, cos, and tan, we can create an AST node that contains a name field and the value the function operates on.

js
Copied! ⭐️ 
{
  type: 'Function',
  name: name,
  value: value
}

Let's now see the finished code for the handlePop function that contains all of these adjustments.

js
Copied! ⭐️ 
function handlePop() {
  const op = stack.pop()

  if (op === '(')
    return

  if (op === 'u') {
    return {
      type: 'UnaryExpression',
      value: -Number.parseFloat(output.pop().value),
    }
  }

  if (isFunction(op))
    return { type: 'Function', name: op, value: output.pop() }

  const right = output.pop()
  const left = output.pop()

  if (opSymbols.includes(op)) {
    return {
      type: 'BinaryExpression',
      operator: op,
      left,
      right,
    }
  }
}

Not so bad so far, right? However, we still need to build an AST for numbers. In the handleToken function, we currently have the following code:

js
Copied! ⭐️ 
switch (true) {
  case !isNaN(parseFloat(token)):
    addToOutput(token);
    break;

When we encounter a number token, we need push an AST node instead of just a number.

js
Copied! ⭐️ 
case !isNaN(parseFloat(token)):
  addToOutput({ type: 'Number', value: parseFloat(token) });
  break;

Therefore, numbers will have the following AST node representation:

js
Copied! ⭐️ 
{
  type: 'Number',
  value: value
}

Finished Code

After making all these changes to our implementation of the shunting yard algorithm, we now have the ability to create abstract syntax trees! Let's look at the finished code below.

js
Copied! ⭐️ 
const TokenTypes = {
  NUMBER: 'NUMBER',
  IDENTIFIER: 'IDENTIFIER',
  ADDITION: '+',
  SUBTRACTION: '-',
  MULTIPLICATION: '*',
  DIVISION: '/',
  EXPONENTIATION: '^',
  PARENTHESIS_LEFT: '(',
  PARENTHESIS_RIGHT: ')',
}

const TokenSpec = [
  [/^\s+/, null],
  [/^(?:\d+(?:\.\d*)?|\.\d+)/, TokenTypes.NUMBER],
  [/^[a-z]+/, TokenTypes.IDENTIFIER],
  [/^\+/, TokenTypes.ADDITION],
  [/^\-/, TokenTypes.SUBTRACTION],
  [/^\*/, TokenTypes.MULTIPLICATION],
  [/^\//, TokenTypes.DIVISION],
  [/^\^/, TokenTypes.EXPONENTIATION],
  [/^\(/, TokenTypes.PARENTHESIS_LEFT],
  [/^\)/, TokenTypes.PARENTHESIS_RIGHT],
]

class Tokenizer {
  constructor(input) {
    this.input = input
    this.cursor = 0
  }

  hasMoreTokens() {
    return this.cursor < this.input.length
  }

  match(regex, inputSlice) {
    const matched = regex.exec(inputSlice)
    if (matched === null)
      return null

    this.cursor += matched[0].length
    return matched[0]
  }

  getNextToken() {
    if (!this.hasMoreTokens())
      return null

    const inputSlice = this.input.slice(this.cursor)

    for (const [regex, type] of TokenSpec) {
      const tokenValue = this.match(regex, inputSlice)

      if (tokenValue === null)
        continue

      if (type === null)
        return this.getNextToken()

      return {
        type,
        value: tokenValue,
      }
    }

    throw new SyntaxError(`Unexpected token: "${inputSlice[0]}"`)
  }
}

const operators = {
  'u': {
    prec: 4,
    assoc: 'right',
  },
  '^': {
    prec: 4,
    assoc: 'right',
  },
  '*': {
    prec: 3,
    assoc: 'left',
  },
  '/': {
    prec: 3,
    assoc: 'left',
  },
  '+': {
    prec: 2,
    assoc: 'left',
  },
  '-': {
    prec: 2,
    assoc: 'left',
  },
}

const functionList = ['sin', 'cos', 'tan']

function assert(predicate) {
  if (predicate)
    return
  throw new Error('Assertion failed due to invalid token')
}

function isFunction(token) {
  return functionList.includes(token.toLowerCase())
}

function generateAST(input) {
  const opSymbols = Object.keys(operators)
  const stack = []
  const output = []

  const peek = () => {
    return stack.at(-1)
  }

  const addToOutput = (token) => {
    output.push(token)
  }

  const handlePop = () => {
    const op = stack.pop()

    if (op === '(')
      return

    if (op === 'u') {
      return {
        type: 'UnaryExpression',
        value: output.pop(),
      }
    }

    if (isFunction(op))
      return { type: 'Function', name: op, value: output.pop() }

    const right = output.pop()
    const left = output.pop()

    if (opSymbols.includes(op)) {
      return {
        type: 'BinaryExpression',
        operator: op,
        left,
        right,
      }
    }
  }

  const handleToken = (token) => {
    switch (true) {
      case !isNaN(Number.parseFloat(token)):
        addToOutput({ type: 'Number', value: Number.parseFloat(token) })
        break
      case isFunction(token):
        stack.push(token)
        break
      case opSymbols.includes(token):
        const o1 = token
        let o2 = peek()

        while (
          o2 !== undefined
          && o2 !== '('
          && (operators[o2].prec > operators[o1].prec
          || (operators[o2].prec === operators[o1].prec
          && operators[o1].assoc === 'left'))
        ) {
          addToOutput(handlePop())
          o2 = peek()
        }
        stack.push(o1)
        break
      case token === '(':
        stack.push(token)
        break
      case token === ')':
        let topOfStack = peek()
        while (topOfStack !== '(') {
          assert(stack.length !== 0)
          addToOutput(handlePop())
          topOfStack = peek()
        }
        assert(peek() === '(')
        handlePop()
        topOfStack = peek()
        if (topOfStack && isFunction(topOfStack))
          addToOutput(handlePop())

        break
      default:
        throw new Error(`Invalid token: ${token}`)
    }
  }

  const tokenizer = new Tokenizer(input)
  let token
  let prevToken = null
  while ((token = tokenizer.getNextToken())) {
    if (
      token.value === '-'
      && (prevToken === null
      || prevToken.value === '('
      || opSymbols.includes(prevToken.value))
    )
      handleToken('u')
    else
      handleToken(token.value)

    prevToken = token
  }

  while (stack.length !== 0) {
    assert(peek() !== '(')
    addToOutput(handlePop())
  }

  return output[0]
}

We can then pass an input into our generateAST function, formerly known as evaluate, to generate an abstract syntax tree representation of a math expression! Cool!

js
Copied! ⭐️ 
const input = '1 + 2 * 3'
const result = generateAST(input)
console.log(result)

The result will be the following AST:

js
Copied! ⭐️ 
{
  type: 'BinaryExpression',
  operator: '+',
  left: { type: 'Number', value: 1 },
  right: {
    type: 'BinaryExpression',
    operator: '*',
    left: { type: 'Number', value: 2 },
    right: { type: 'Number', value: 3 }
  }
}

Why use Abstract Syntax Trees?

At this point, you might be wondering why we care so much about abstract syntax trees. For the purpose of building a calculator, it might not seem that useful, but it's still good to know how to make them!

Building an AST is extremely useful for when we might want to build a small programming language. ASTs are also very useful for code transformation or code generation such as when we want to make any sort of transformation to source code or input. Tools like ESLint and Prettier use ASTs to format code or detect any issues in JavaScript or TypeScript syntax.

Another advantage of building ASTs is for creating an intermediate representation (IR) of source code. We can store math expressions as tree data structures and then evaluate them later. Therefore, we can reuse the same AST for different tasks. We can also let the user decide how they want to handle the evaluation logic.

The Visitor Pattern

Once we build an AST and store it somewhere, we can use the visitor pattern to visit every node in the tree and perform an action depending on the node type.

Let's use our generateAST function we built in this tutorial to generate an AST for the expression, -1 + 2 * sin(3.14).

js
Copied! ⭐️ 
const input = '-1 + 2 * sin(3.14)'
const ast = generateAST(input)
console.log(ast)

This will produce the following AST:

js
Copied! ⭐️ 
{
  type: 'BinaryExpression',
  operator: '+',
  left: { type: 'UnaryExpression', value: { type: 'Number', value: 1 } },
  right: {
    type: 'BinaryExpression',
    operator: '*',
    left: { type: 'Number', value: 2 },
    right: {
      type: 'Function',
      name: 'sin',
      value: { type: 'Number', value: 3.14 }
    }
  }
}

Using this AST, we can choose to evaluate the math expression, reconstruct the original math expression, or transform the AST into another AST. Each task can be done easily by using the visitor design pattern.

js
Copied! ⭐️ 
class NodeVisitor {
  visit(node) {
    switch (node.type) {
      case 'Number':
        return this.visitNumber(node)
      case 'BinaryExpression':
        return this.visitBinaryExpression(node)
      case 'UnaryExpression':
        return this.visitUnaryExpression(node)
      case 'Function':
        return this.visitFunction(node)
    }
  }

  visitNumber(node) {
    return node.value
  }

  visitBinaryExpression(node) {
    switch (node.operator) {
      case '+':
        return this.visit(node.left) + this.visit(node.right)
      case '-':
        return this.visit(node.left) - this.visit(node.right)
      case '*':
        return this.visit(node.left) * this.visit(node.right)
      case '/':
        return this.visit(node.left) / this.visit(node.right)
      case '^':
        return this.visit(node.left) ** this.visit(node.right)
      default:
        throw new Error(`Invalid operation: ${node.operator}`)
    }
  }

  visitUnaryExpression(node) {
    return -this.visit(node.value)
  }

  visitFunction(node) {
    switch (node.name) {
      case 'sin':
        return Math.sin(this.visit(node.value))
      case 'cos':
        return Math.cos(this.visit(node.value))
      case 'tan':
        return Math.tan(this.visit(node.value))
      default:
        throw new Error(`Invalid function: ${node.name}`)
    }
  }
}

Notice how we call the visit method recursively until we eventually reach the visitNumber function. Once we build the NodeVisitor class, we can then use it to evaluate our AST:

js
Copied! ⭐️ 
const input = '-1 + 2 * sin(3.14)'
const ast = generateAST(input)
const visitor = new NodeVisitor()
const result = visitor.visit(ast)
console.log(result) // -0.9968146941670264

In our implementation of the visitor design pattern, we are creating a visitor for each node type and performing a mathematical operation based on that node type. Inside each visitor, we could have done something different though. We could have logged information to a database, logged information to the console, or even make number-shaped balloons appear on the screen 🎈

Instead of changing the internals of our shunting yard algorithm implementation, we now just have to change the logic inside each visitor. Super cool! 😎

Conclusion

In this tutorial, we learned how to build abstract syntax trees using the shunting yard algorithm! We have now used the shunting yard algorithm to perform three different tasks:

  1. Converting infix notation to RPN/postfix form
  2. Evaluating math expressions in infix form
  3. Generating abstract syntax trees

Most of the changes were done in the handlePop function with small changes to other functions. By leveraging a stack, it's easy to keep track of the order of operations. Then, we can pop items off the stack to either perform computations or build constructs such as abstract syntax trees to defer execution until later. Once we have abstract syntax trees, we can use the visitor design pattern to evaluate the AST or perform some other action. The abstract syntax tree helps us separate the data structure logic from the evaluation logic. By giving users access to an abstract syntax tree, it lets them decide how they want to evaluate math expressions.

I hope you've enjoyed my math expression parser series so far! 😊 We've spent a lot of time discussing how to build a math expression parser and evaluator using the shunting yard algorithm. In the next tutorial, we'll move away from the shunting yard algorithm and learn how to build a math expression parser using a parser generator! Happy coding! 🙂

Previous
Handling Unary Operations in the Shunting Yard Algorithm
Next
Parser Generators for Math Expressions
✨ See All Posts ✨