How to Build a Math Expression Parser in JavaScript
Greetings, friends! I've recently been interested in parser theory, compiler design, and interpreter design. Such fascinating topics! Yes, nerdy topics I know, but all programming languages are built on top of this important information. Parser theory is rarely talked about, and I love talking about obscure topics on my website and condensing them down into simple language. Parser theory is complex, but I'm here to make it easier to understand. Let's begin!
Introduction
In my next series of posts, we will learn how to make a math expression parser that can take math expressions such as 1 + 2 * 3 and return a result such as 7 that correctly follows the order of operations.
You may be wondering, "Why can't we use the eval function in JavaScript to parse and evaluate mathematical expressions?" The reason is that the eval function is extremely dangerous to use in production code and suffers from many problems.
It doesn't matter if you use eval in the browser or in Node.js, this function is a giant security risk because it allows malicious users to execute arbitrary code. Therefore, it's better to create our own parser that can safely parse and evaluate mathematical expressions!
In this tutorial series, I won't show you just one way of making a math expression parser. I'll introduce you to the world of parser theory by making a math expression parser in multiple ways:
- Reverse Polish Notation (RPN) Evaluator
- Shunting Yard Algorithm
- LL Parser Generator
- LR Parser Generator
- PEG Parser Generator
- Recursive Descent Parser
- Pratt Parser
We'll start this series by building a math expression evaluator/calculator that accepts input in the form of Reverse Polish notation (RPN), also known as postfix notation. Examples of RPN/postfix form include strings such as 1 2 +.
Next, we'll use the Shunting yard Algorithm to build a math expression parser that can accept inputs in the standard infix notation such as 1 + 2.
Then, we'll learn how to use parser generators that can accept different types of "grammars." I'll talk about "grammars" in great detail later in this tutorial series.
Finally, we'll create complex parsers by hand using recursive descent parsing and pratt parsing.
What are Parsers?
Parsers are programs that can process text and perform syntactic analysis, which means analyzing a string of symbols and doing something useful with them. Each symbol can represent something abstract like the keywords in JavaScript such as the if or for symbols. Strings and numbers in JavaScript could be considered symbols as well. Basically, any type of information that can be grouped together can be considered a symbol. By themselves, the letters i and f, don't provide much value. However, if is definitely a valid keyword in JavaScript, so we consider it a meaningful symbol. Symbols are often referred as "tokens" in parser design. Mathematical symbols such as +, -, *, and / can be considered valid tokens.
Parsers are commonly used to read code or text and do something meaningful with them. For example, this webpage uses HTML, which is a type of XML. The browser has a parser that understands how to parse HTML code such as <h1>My Awesome Header</h1> and render a header element that has large font (unless changed through CSS styling). The browser also has a separate parser that scans through CSS code to apply styling and make the webpage look pretty. Browsers use multiple types of parsers, each dedicated to a particular language. The most common parsers used by the browser include a HTML parser, CSS parser, and JavaScript parser.
Abstract Syntax Trees (AST)
Browsers have JavaScript engines such as V8 (for Google Chrome) that understand how to parse JavaScript code, turn it into an abstract syntax tree (AST), and evaluate it. When you run console.log(1 + 2 * 3) in the Google Chrome browser, the V8 engine understands that it should evaluate the math expression and display a value of 7 in the console. Many parsers that are used for programming languages generate abstract syntax trees, so math expressions can be evaluated in the correct order. Let's look at an example of an abstract syntax tree for 1 + 2 * 3.
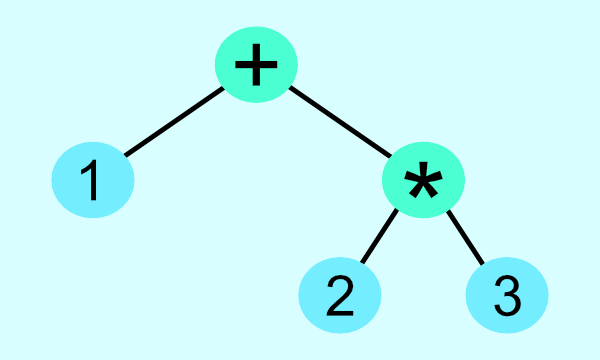
The top node has the lowest priority, and the bottom nodes of the tree have the highest priority. As we can see from the AST above, multiplication is applied first followed by addition.
1 + 2 * 3 = 1 + 6 = 7
Let's now look at a more complex math expression that utilizes parentheses and exponents:
(1 + 2 * (4 / 2) ^ 2 ^ 3) - 1
If we threw this math expression into Google, we'd see that the answer equals 512. You can also use JavaScript to verify the result is correct.
const result = (1 + 2 * (4 / 2) ** 2 ** 3) - 1
console.log(result) // 512
If we built an AST for this math expression, it would look similar to the following:
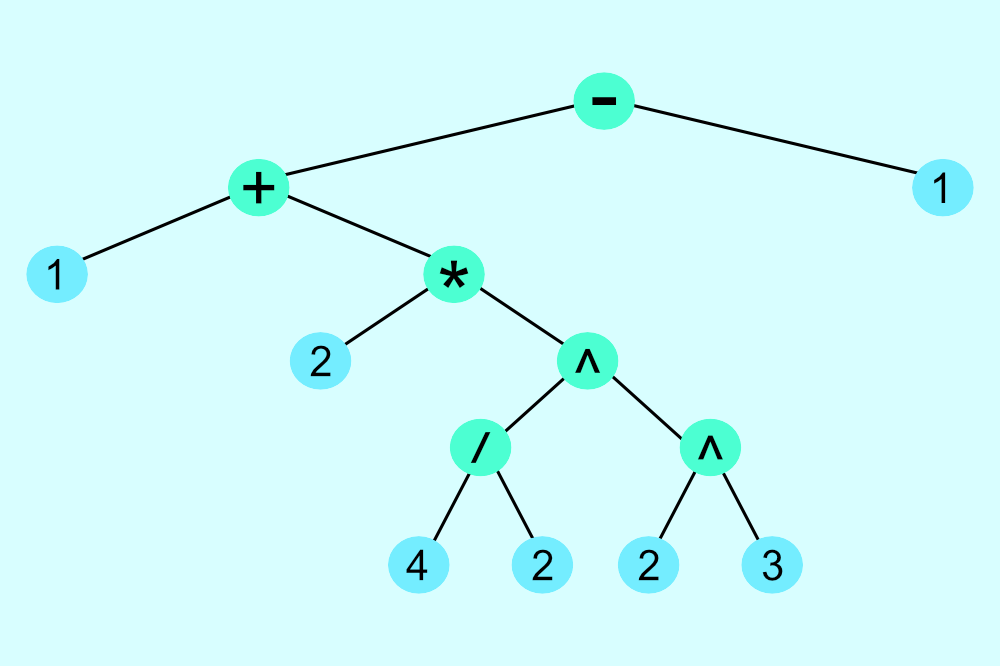
As we can see, the AST grows larger as more operations are applied. As mentioned earlier, the top node has the lowest priority, and the bottom nodes of the tree have the highest priority. The parentheses actually play a big part in determining order of operations.
The order of operations is as follows:
- Parentheses
- Exponents (evaluated from right to left)
- Multiplication/Division (evaluated from left to right)
- Addition/Subtraction (evaluated from left to right)
You may have heard of the mnemonic, "Please Excuse My Dear Aunt Sally" (PEMDAS). This is a common phrase that helps people memorize the order of operations.
- P = Parentheses
- E = Exponents
- M = Multiplication
- D = Division
- A = Addition
- S = Subtraction
Let's apply the order of operations to solve the math expression:
(1 + 2 * (4 / 2) ^ 2 ^ 3) - 1
= (1 + 2 * 2 ^ 2 ^ 3) - 1
= (1 + 2 * 2 ^ 8) - 1
= (1 + 2 * 256) - 1
= (1 + 512) - 1
= 513 - 1
= 512
It's interesting to note that a lot of popular modern programming languages don't use the caret symbol, ^, for exponentiation, but you'll learn how to make a math expression parser that understands this symbol by the end of this tutorial series 😄
Practically all programming languages and domain-specific languages (DSL) need some kind of parser that can ensure the mathematical operations are applied in the correct order. However, parsers are used for many other types of operations, not just mathematical expression evaluation. When parsing a programming language, the parsers inside compilers or interpreters generate ASTs that include information about the entire program, including if statements, for loop statements, and more.
This tutorial series will focus on only building a math expression parser and evaluator. In a later series, I'll discuss how to parse and build a tiny programming language, but it's helpful to know how to parse math expressions first.
Conclusion
In the next article, we'll build a reverse polish notation (RPN) calculator/evaluator. Then, we'll build an implementation of the Shunting Yard algorithm that can convert an expression written in infix form to RPN/postfix form. We'll also learn how to use the Shunting yard algorithm to evaluate expressions without the need of RPN/postfix form. Lots to cover and lots to learn! Happy coding!